Mathematics: Change of subject of formular

Change of Subject Formula

Whenever the subject of a formula is to be changed, the intention is to make the value becoming the subject stand alone and remain on the left hand side of the expression. The methods used to effect this change may be any basic mathematical principles like multiplication, addition, subtraction, division, finding square roots, etc.

Whatever operation that is used to perform the change must be applied to both sides of the expression (formula).

Examples;
1. Make u the subject of the formula; v2 = u2 + 2as.





Solution

Step 1

Rearrange by bringing “u2” to the LHS of the expression and carrying v2 to the RHS of the expression. The reason for this is because you have been instructed to make “u” the subject of the formula according to the question.

-u2 = 2as – v2

Note;
Whenever you carry figures from one side of an expression to another, the sign changes to the opposite.

Step 2

Multiply both sides by -1 in order to eliminate the – (minus sign);

u2 = 2as + v2

Step 3

Take square root of both sides;




2. Change the subject of the formula below to h;

Solution

Step 1

The target value here is “h”. So in order to make “h” subject, you need to remove the square root by taking square of both sides;






Step 2

Cross multiply both sides;





2Qh = 100p2

Step 3

Divide both sides by 2Q;






Final answer will be;
3. Express S in terms of T, X and K in the formula below;




Solution

Step 1

Remove the square root by taking square of both sides;









Step 2

Split the RHS expression apart to make it easier for you to solve. See below;







Step 3

Expand (2X) ² and remove the square root;





Note; raise to power of 2 can easily cancel square root. This is why: (2 × ½ gives 1 where ½ is the mathematical interpretation of square root)









Step 4

Cross multiply both sides;
4SX² X 1 = T² X K
4SX² = KT²

Step 5

Divide both sides by 4X² because you need “S” to be alone;












Lastly, we need to find S when T = 8, X = 2 and K = 3. The only way to do this is by substituting for T, X and K respectively in our new formula.


















S = 3 × 4
Note; 16 goes in 64 gives 4
S = 12. (Answer)
Practice these questions below;

1. Make d the subject of the formula below; 








2. Make m the subject of the expression below;








3. Make v the subject of the relation;







4. Given that v2 = u2 + 2as, express a in terms of u, v and s. Hence, find the value of a when u = 15, v = 20 and s = 5.

5. An expression is given as

Make R the subject of the formula and find R when K = 20, q = 15 and D = 6.

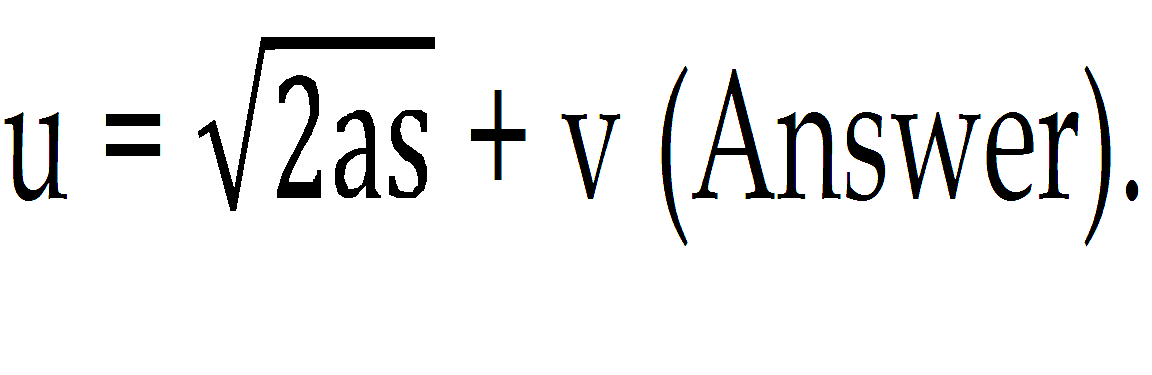
Comments

Post a Comment

Popular posts from this blog

PEAR

What's New and Beneficial About Pears For nutritional reasons, we're often advised to consume the skins of fruits. However, it's less often that research provides strong evidence in support of this advice. Recent studies have shown that the skin of pears contains at least three to four times as many phenolic phytonutrients as the flesh. These phytonutrients include antioxidant, anti-inflammatory flavonoids, and potentially anti-cancer phytonutrients like cinnamic acids. The skin of the pear has also been show to contain about half of the pear's total dietary fiber. In recent studies measuring risk of type 2 diabetes in U.S. women, pears have earned very special recognition. Researchers now know that certain flavonoids in food can improve insulin sensitivity, and of special interest in this area have been three groups of flavonoids (flavonols, flavan-3-ols, and anthocyanins). All pears contain flavonoids falling within the first two groups, and red-skinned pe
Read more

Aubauf Method - Building Up

Image
Atoms Are Built Up by Adding Electrons Although the nucleus of an atom is very dense, the electrons around it can take on a variety of positions which can be summarized as an electron configuration. An element's electron configuration can be represented using energy level diagrams, or Aufbau diagrams. The Aufbau principle (from the German Aufbau meaning "building up, construction") describes a model-building method in which an atom is "built up" by progressively adding electrons. As electrons are added, they assume the most stable shells with respect to the nucleus and the electrons already present. Filling in an Aufbau Diagram The order in which orbitals are filled is given by the Madelung rule. The rule is based on the total number of nodes in the atomic orbital, n + ℓ, which is related to the energy. In this context, n represents the principal quantum number and ℓ represents the azimuthal quantum number. The values ℓ = 0, 1, 2, 3 correspo
Read more
Image
Building Self-Confidence Preparing Yourself for Success! Learn how to become more self-confident with James Manktelow and Amy Carlson. From the quietly confident doctor whose advice we rely on, to the charismatic confidence of an inspiring speaker, self-confident people have qualities that everyone admires. Self-confidence is extremely important in almost every aspect of our lives, yet so many people struggle to find it. Sadly, this can be a vicious circle: people who lack self-confidence can find it difficult to become successful. After all, most people are reluctant to back a project that's being pitched by someone who was nervous, fumbling, and overly apologetic. On the other hand, you might be persuaded by someone who speaks clearly, who holds his or her head high, who answers questions assuredly, and who readily admits when he or she does not know something. Confident people inspire confidence in others: their audience, their peers, their bosses, their customers, and
Read more